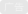
LTspice可用于对复杂电路进行统计容差分析。本文介绍在LTspice中使用蒙特卡罗和高斯分布进行容差分析和最差情况分析的方法。为了证实该方法的有效性,我们在LTspice中对电压调节示例电路进行建模,通过内部基准电压和反馈电阻演示蒙特卡罗和高斯分布技术。然后,将得出的仿真结果与最差情况分析仿真结果进行比较。其中包括4个附录。附录A提供了有关微调基准电压源分布的见解。附录B提供了LTspice中的高斯分布分析。附录C提供了LTspice定义的蒙特卡罗分布的图形视图。附录D提供关于编辑LTspice原理图和提取仿真数据的说明。
本文介绍可以使用LTspice进行的统计分析。这不是对6-sigma设计原则、中心极限定理或蒙特卡罗采样的回顾。
在系统设计中,为了保证设计成功,必须考虑参数容差约束。有一种常用方法是使用最差情况分析(WCA),在进行这种分析时,将所有参数都调整到最大容差限值。在最差情况分析中,会分析系统的性能,以确定最差情况的结果是否在系统设计规格范围内。最差情况分析的效力有一些局限性,例如:
进行系统容差分析的另一种替代方法是使用统计工具来进行元件容差分析。统计分析的优点在于:得出的数据的分布能够反映出在物理系统中通常需要测量哪些参数。在本文中,我们使用LTspice来仿真电路性能,利用蒙特卡罗和高斯分布来体现参数容差变化,并将其与最差情况分析仿真进行比较。
除了提到的关于最差情况分析的一些问题外,最差情况分析和统计分析都能提供与系统设计相关的宝贵见解。关于如何在使用LTspice时使用最差情况分析的教程,请参见Gabino Alonso和Joseph Spencer撰写的文章“LTspice:利用最少的仿真运行进行最差情况的电路分析”。
图1显示在LTspice中建模的基准电压,使用蒙特卡罗分布。标称电压源为1.25 V,公差为1.5%。蒙特卡罗分布在1.5%的容差范围内,定义251个电压状态。图2显示251个值的直方图,图中包含50个条形区间(bin)。表1表示与该分布相关的统计结果。
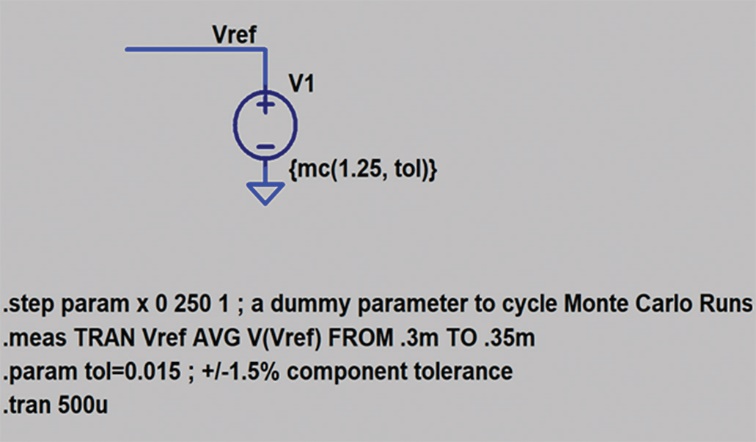
图1.电压源的LTspice原理图(使用蒙特卡罗分布)
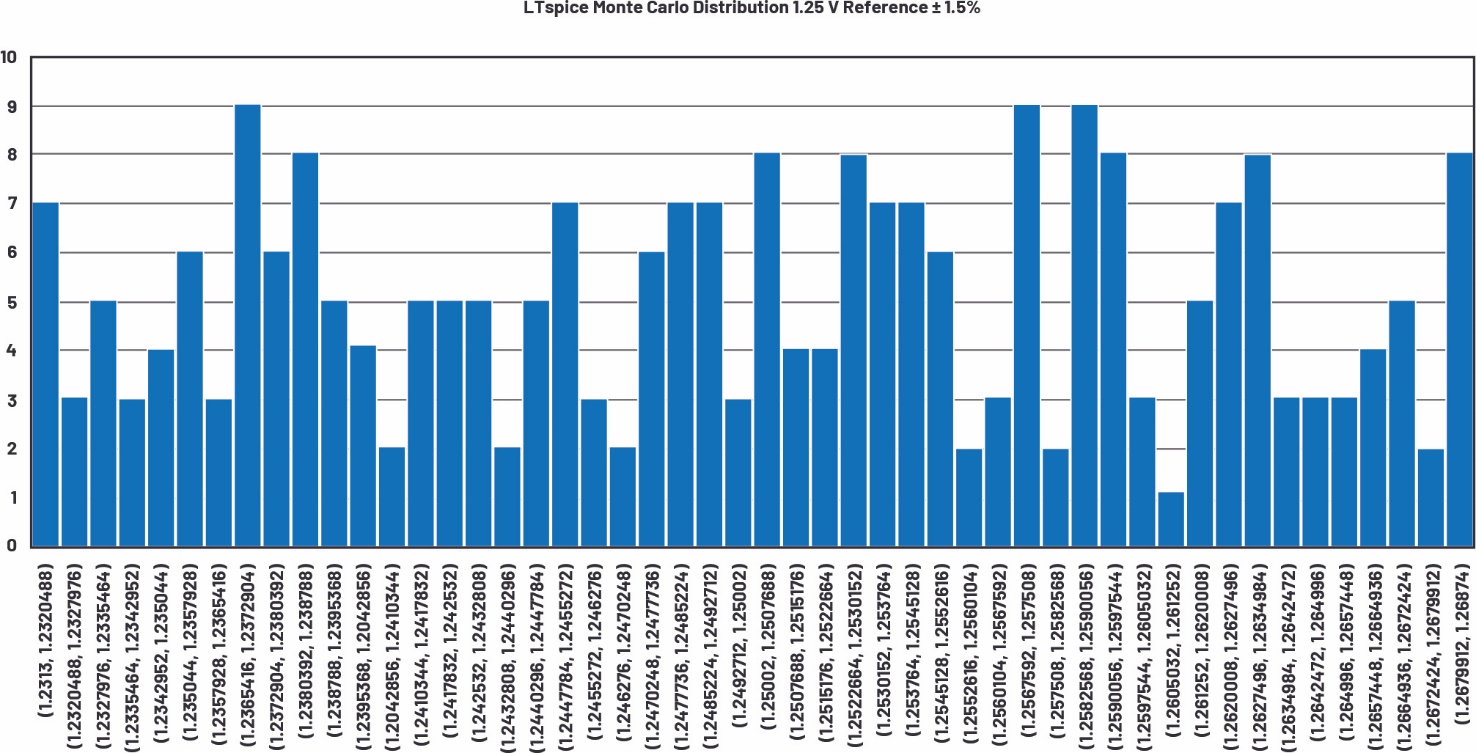
图2.1.25 V基准电压的蒙特卡罗仿真结果,以50个条形区间和251个点组成的直方图呈现
表1.蒙特卡罗仿真结果的统计分析
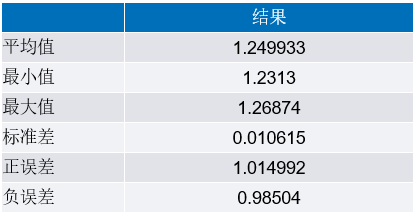
图3显示在LTspice中建模的基准电压,使用高斯分布。标称电压源为1.25 V,容差为1.5%。蒙特卡罗分布在1.5%的容差范围内,定义251个电压状态。图4显示251个值的直方图,图中包含50个条形区间(bin)。表2表示与该分布相关的统计结果。

图3.电压源的LTspice原理图(使用3-sigma高斯分布)
表2.高斯参考仿真结果的统计分析
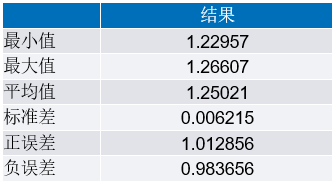
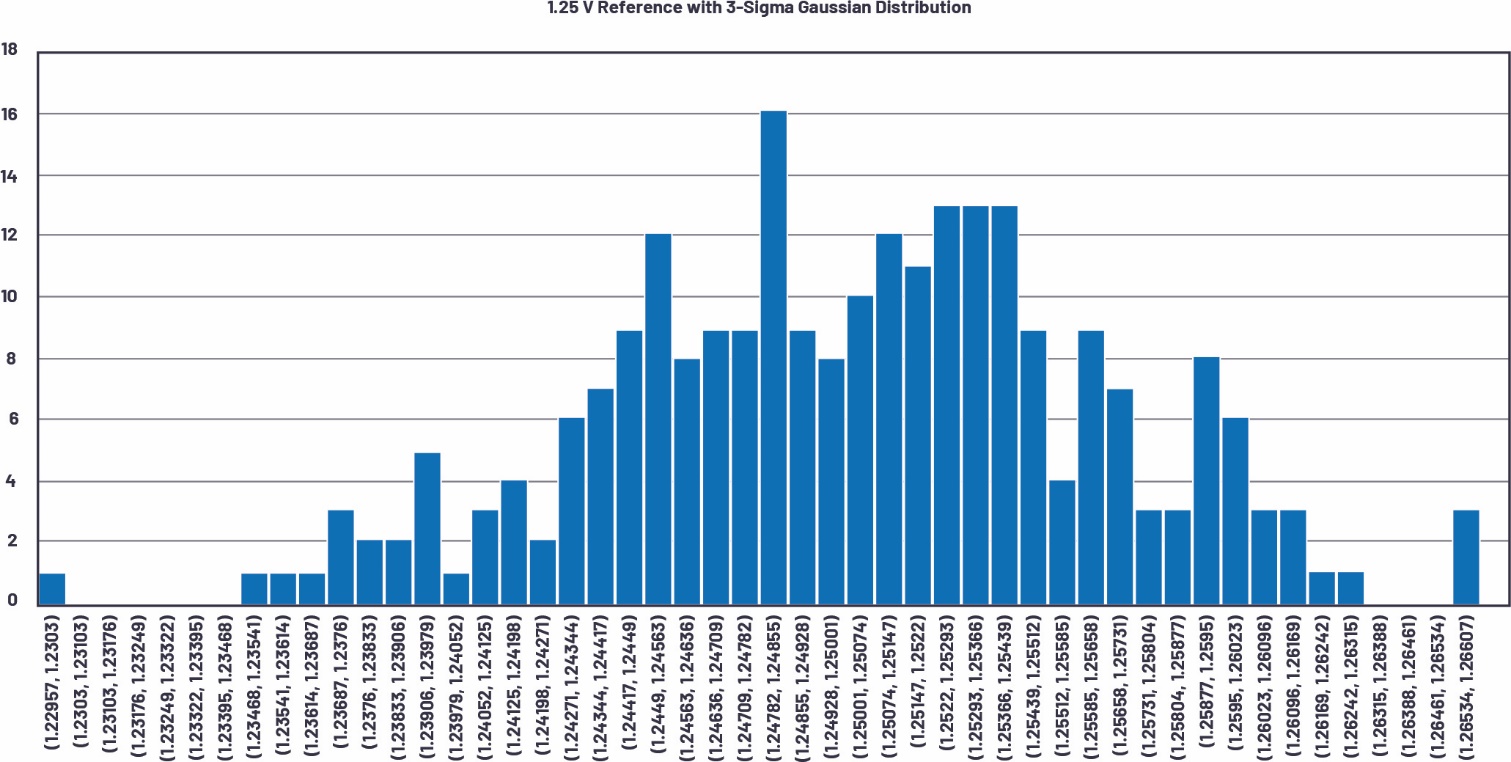
图4.1.25 V基准电压的3-sigma高斯仿真结果,以50个条形区间和251个点组成的直方图呈现
高斯分布是以钟形曲线表示的正态分布,其概率密度如图5所示。
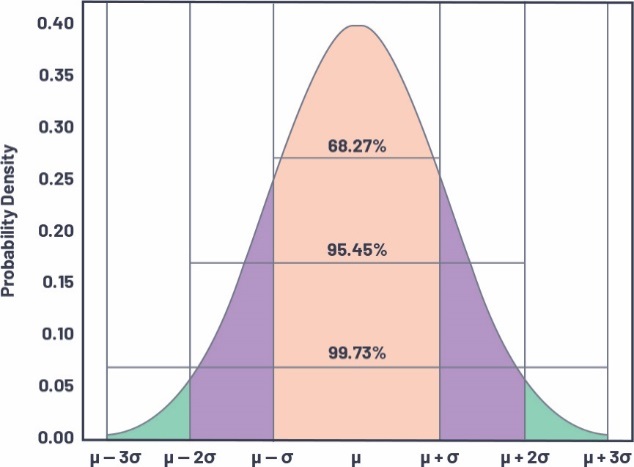
图5.3-sigma高斯正态分布
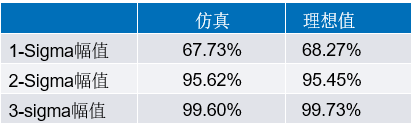
理想分布和LTspice仿真的高斯分布之间的关联如表3所示。
表3.LTspice仿真的251个点高斯分布的统计分布
综上所述,LTspice可用于仿真电压源的高斯或蒙特卡罗容差分布。该电压源可用于对DC-DC转换器中的基准电压进行建模。LTspice高斯分布仿真结果与预测的概率密度分布高度吻合。
图6显示DC-DC转换器的LTspice仿真原理图,使用压控电压源来模拟闭环电压反馈。反馈电阻R2和R3的标称值为16.4 kΩ和10 kΩ。内部基准电压的标称值为1.25 V。在该电路中,标称调节电压VOUT或设定点电压为3.3 V。
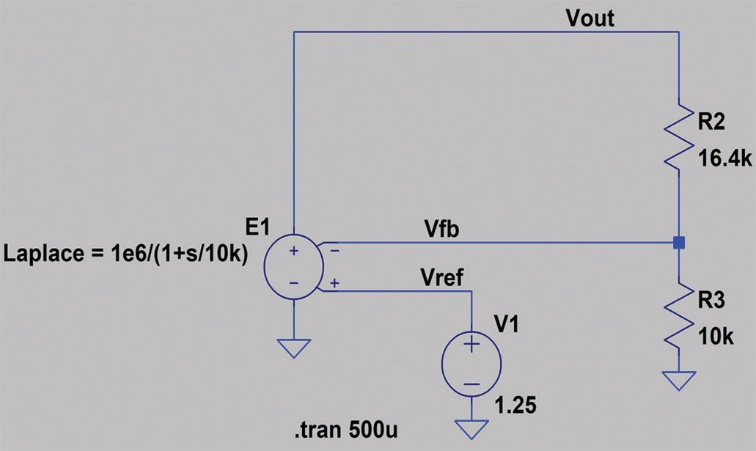
图6.LTspice DC-DC转换器仿真原理图
为了仿真电压调节的容差分析,反馈电阻R2和R3的容差定义为1%,内部基准电压的容差定义为1.5%。本节介绍三种容差分析方法:使用蒙特卡罗分布的统计分析、使用高斯分布的统计分析,以及最差情况分析(WCA)。
图7和图8显示使用蒙特卡罗分布仿真的原理图和电压调节直方图。
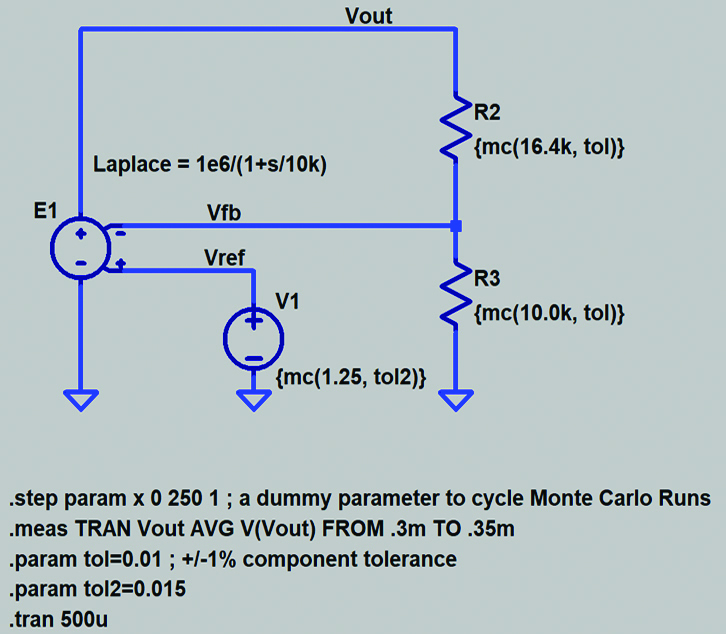
图7.使用蒙特卡罗分布进行容差分析的原理图
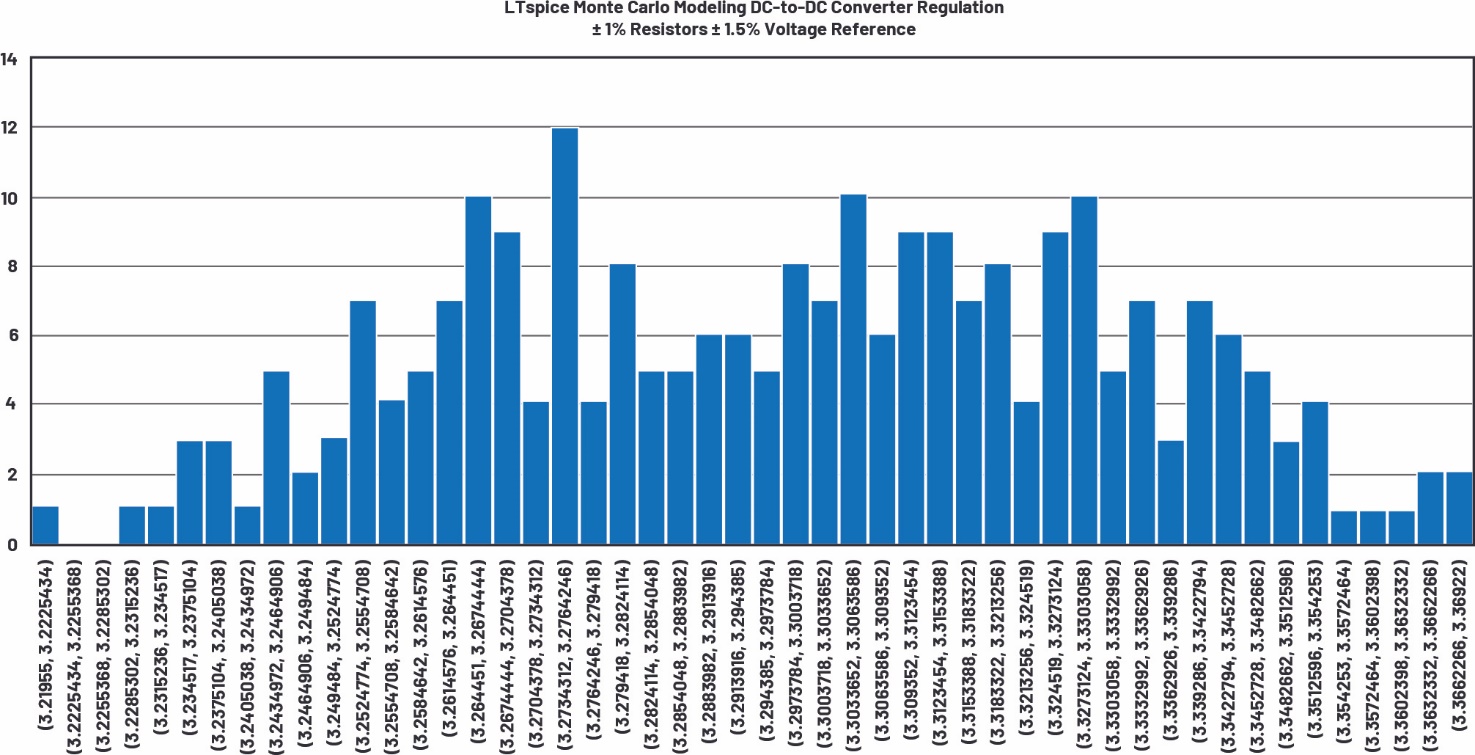
图8.使用蒙特卡罗分布仿真的电压调节直方图
图9和图10显示使用高斯分布仿真的原理图和电压调节直方图。
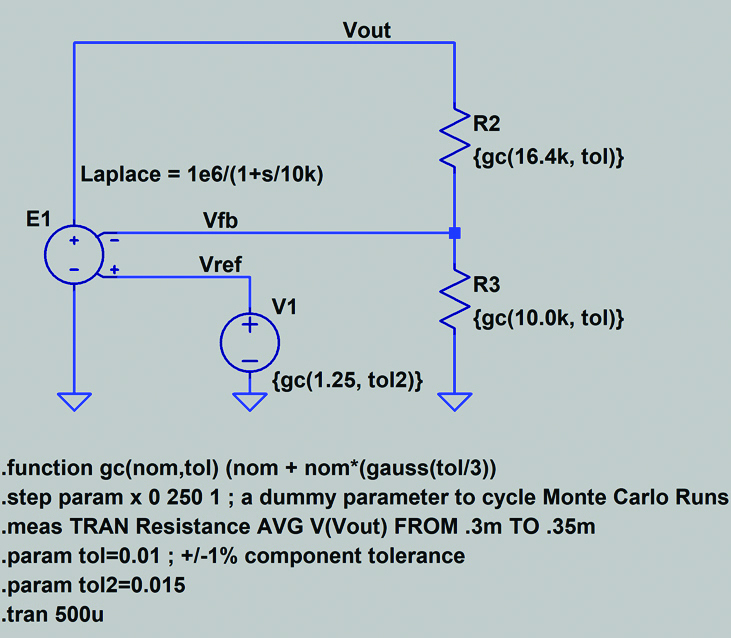
图9.使用高斯分布进行容差分析的原理图
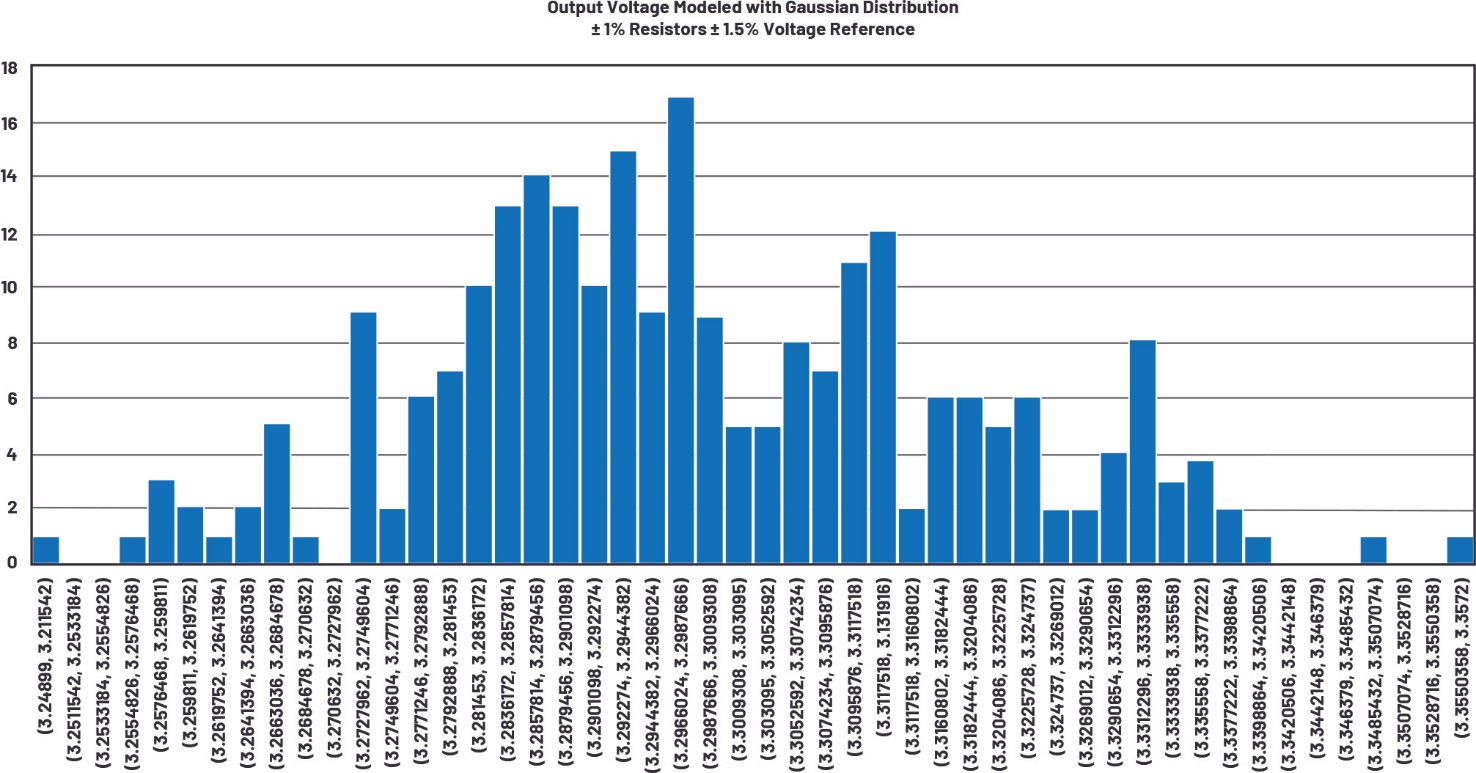
图10.使用高斯分布仿真进行容差分析的直方图
图11和图12显示使用最差情况分析仿真的原理图和电压调节直方图
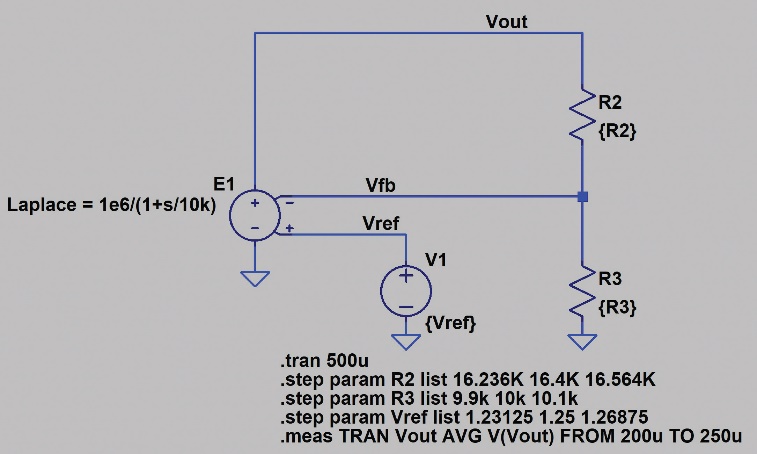
图11.使用最差情况分析仿真进行容差分析的原理图
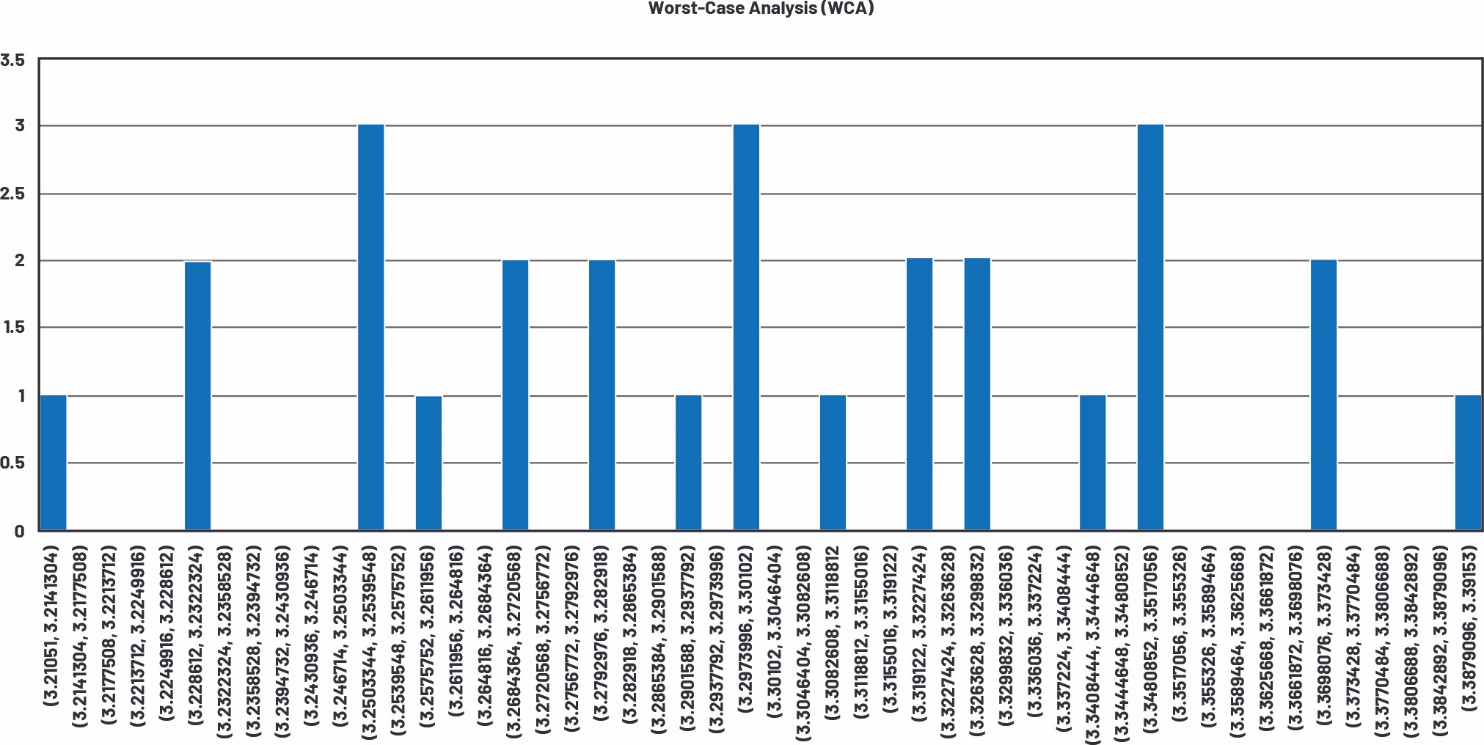
图12.使用WCA进行容差分析的直方图
表4和图13比较了容差分析结果。在这个示例中,WCA预测最大偏差,基于高斯分布的仿真预测最小偏差。具体如图13中的箱形图所示,箱形表示1-sigma限值,盒须表示最小和最大值。
表4.三种公差分析方法的电压调节统计汇总
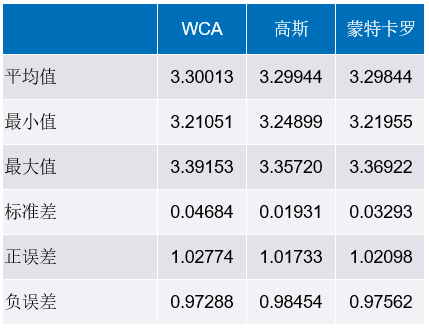
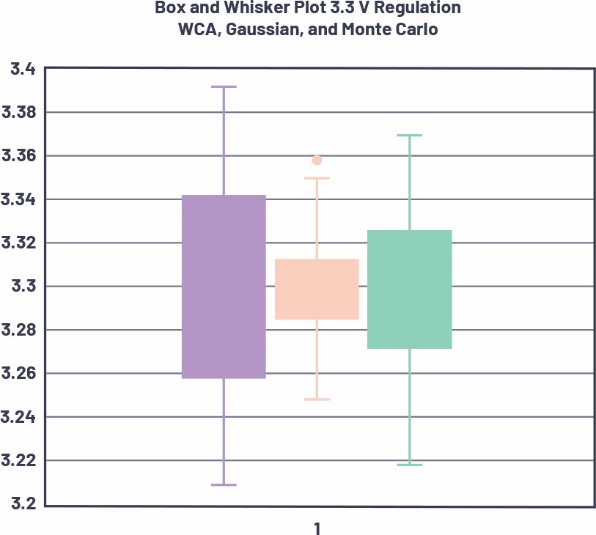
图13.调节电压分布的箱形图比较
本文使用简化的DC-DC转换器模型来分析三种变量,使用两个反馈电阻和内部基准电压来模拟电压设定点调节。使用统计分析来展示得出的电压设定点分布。通过图表来展示结果。并与最差情况计算结果进行比较。由此得出的数据表明,最差情况下的限值在统计学上是不可能的。
仿真均在LTspice中完成。
附录A介绍集成电路中经调节基准电压的统计分布。
在调节前,内部基准电压采用高斯分布,在调节后,采用蒙特卡罗分布。调节过程通常如下所示:
将得到的分布结果与原来的高斯分布相比,可看到有些数值没有变化,而其他数值则尽可能接近理想值。生成的直方图类似于立柱带有弧形顶部,如图14所示。
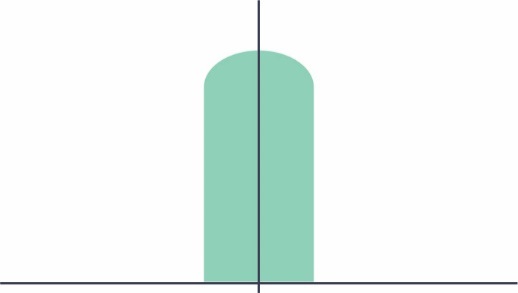
图14.基准电压值在调节后的分布图
虽然这看起来很像是随机分布,但事实并非如此。如果产品是在封装后微调,那么其在室温下的分布图就如图14所示。如果产品是在晶圆分类时进行微调,则组装到塑料封装时上述分布会再次展开(spread out)。其结果通常是歪斜的高斯分布。
附录B简要回顾LTspice中提供的高斯分布命令。将回顾sigma = 0.00333和sigma = 0.002时的分布,以及理想分布和仿真的高斯分布之间的一些数值比较。本附录旨在提供仿真结果的图表和数值分析。
图15显示电阻R1的1001点高斯分布的原理图。
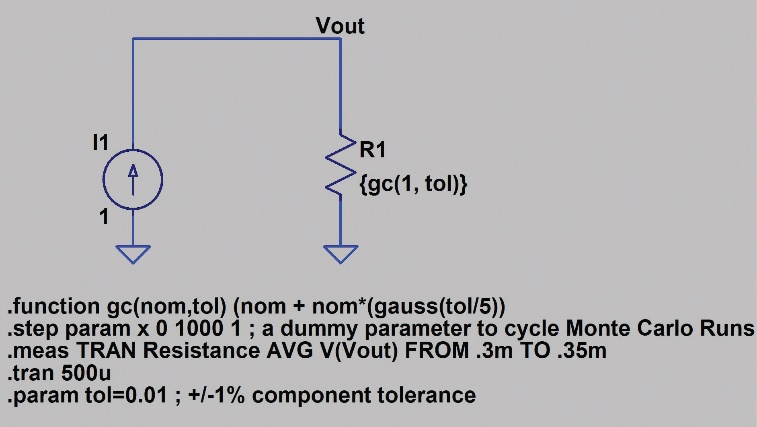
图15.5-sigma高斯分布原理图
值得注意的是对.function语句的修改,将高斯函数的公差定义为tol/5。这导致标准偏差为0.002,或者在1%公差下偏差为1⁄5。直方图如图16所示。
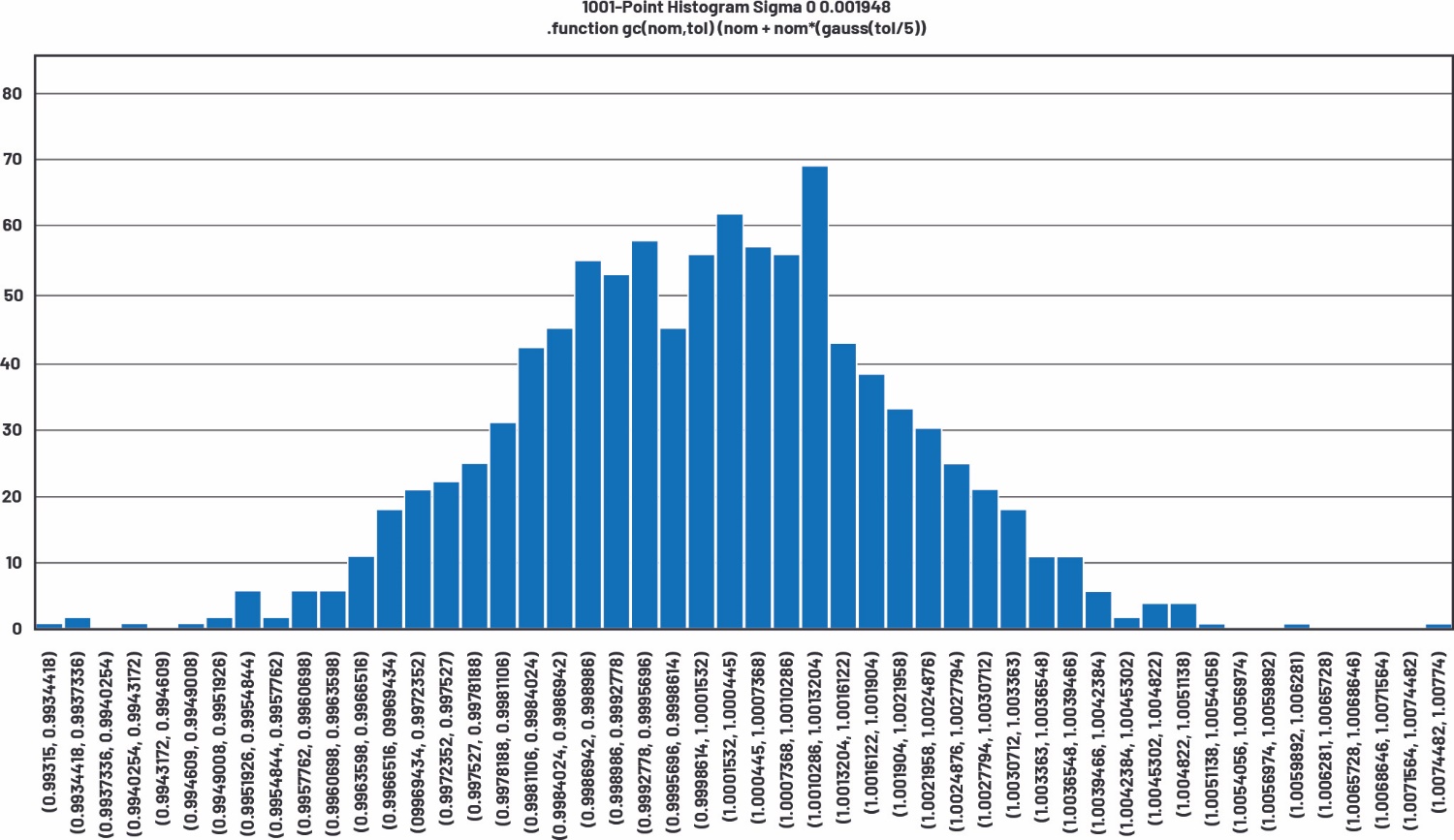
图16.1001点、5-sigma高斯分布的直方图,包含50个条形区间
表5显示1001点仿真的统计分析。值得注意的是,标准偏差为0.001948,而预测偏差为0.002。
表5.5-sigma分布仿真的统计分析
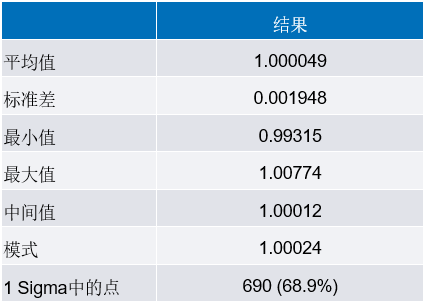
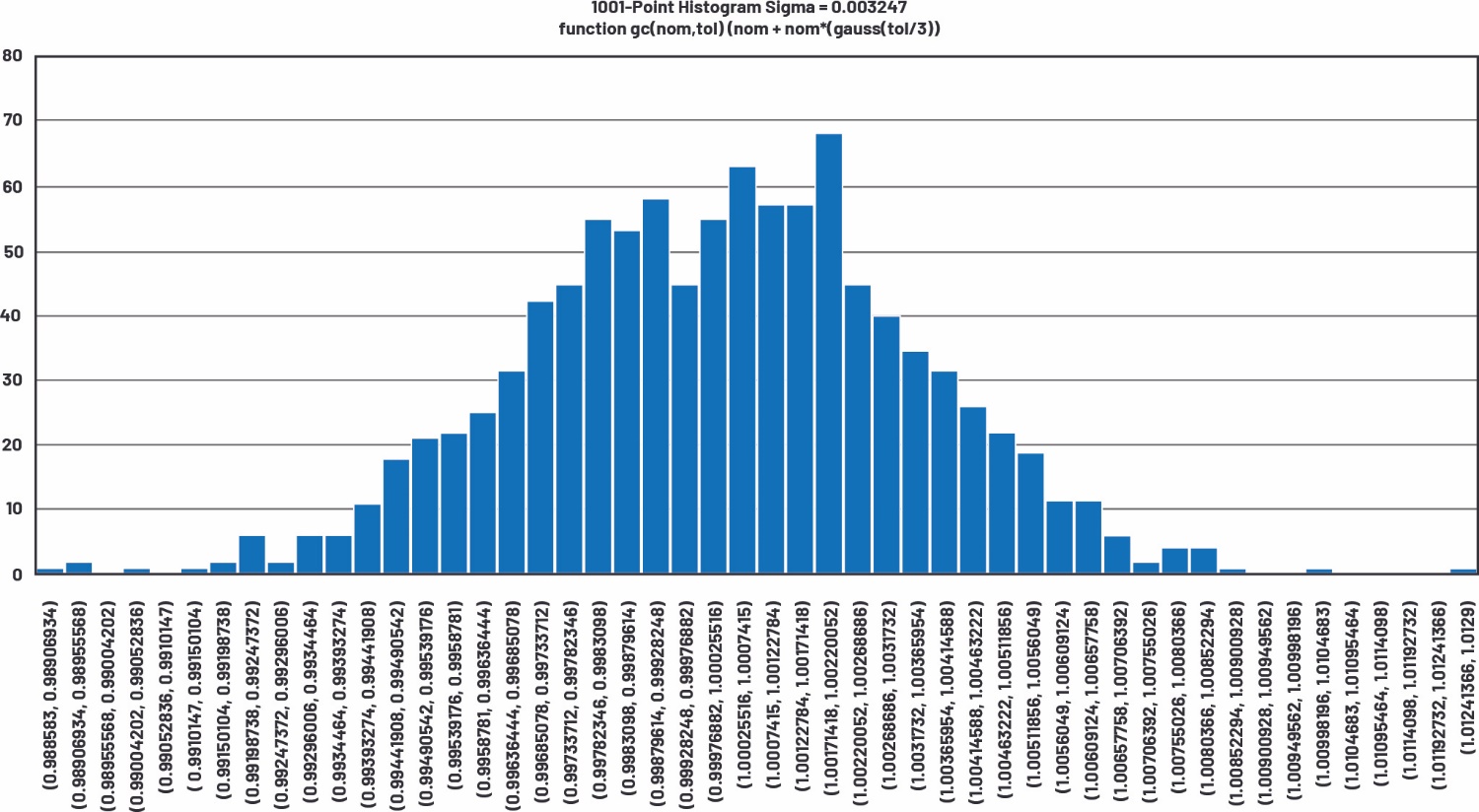
图17.1001点、3-sigma高斯分布的直方图,包含50个条形区间
图17和表6给出了类似的结果,sigma = 0.00333,或者在容差定义为1%时为1⁄3。
表6.3-Sigma高斯分布仿真的统计分析
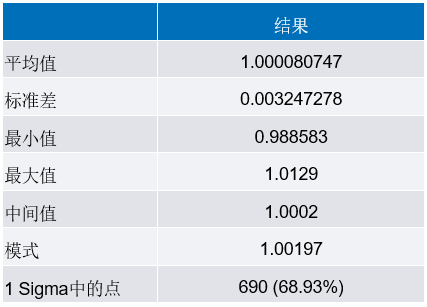
图18至图21以及表7表示1001点蒙特卡罗仿真的原理图。
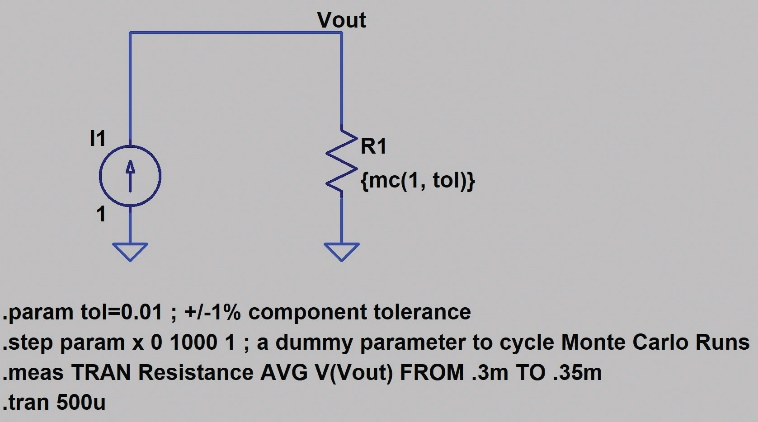
图18.1001点蒙特卡罗分布仿真的LTspice原理图
表7.图18至图21所示的蒙特卡罗分布仿真的统计分析
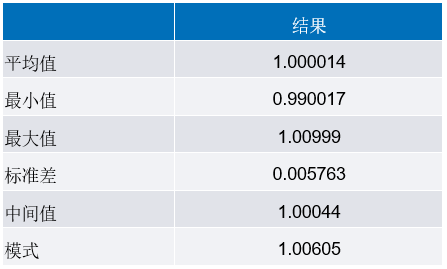
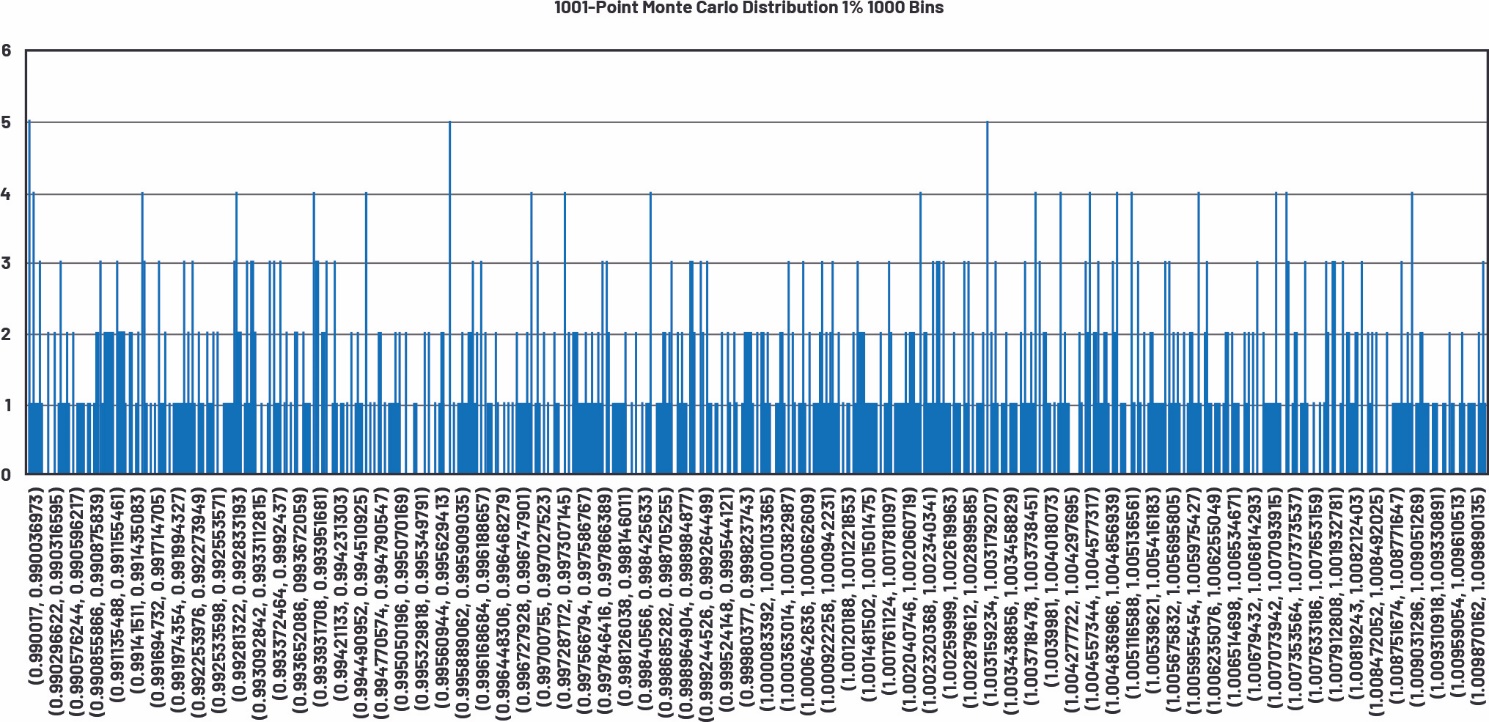
图19.1001点蒙特卡罗分布的1000条形区间直方图
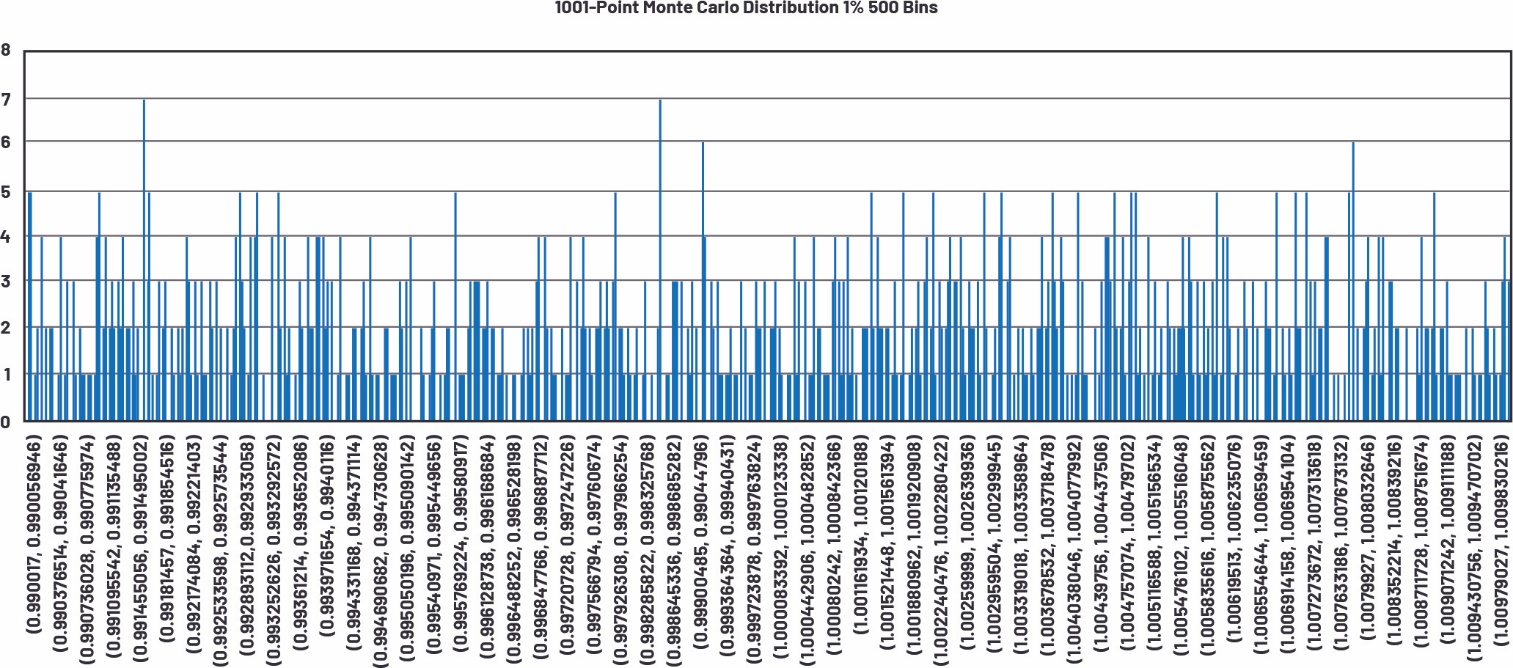
图20.1001点蒙特卡罗分布的500条形区间直方图
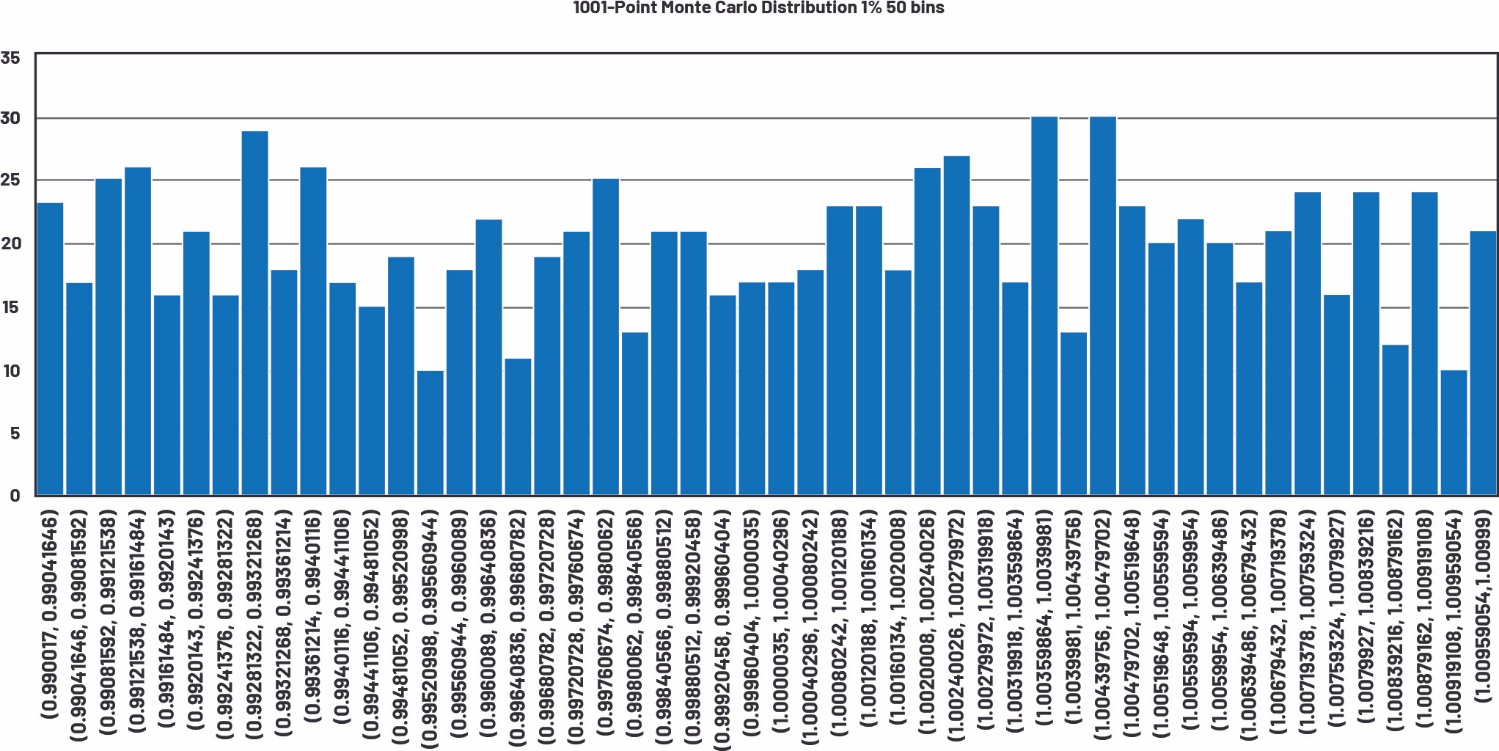
图21.1001点蒙特卡罗分布的50条形区间直方图
附录D回顾:
图22显示蒙特卡罗容差分析的原理图。红色箭头表示在.param语句中定义的元件的容差。.param语句属于SPICE指令。
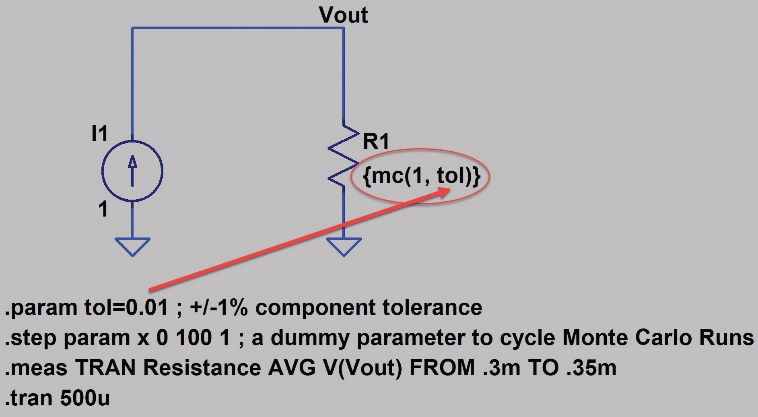
图22.LTspice中的蒙特卡罗容差分析
可以右键单击元件来编辑R1的电阻值。如图23所示。
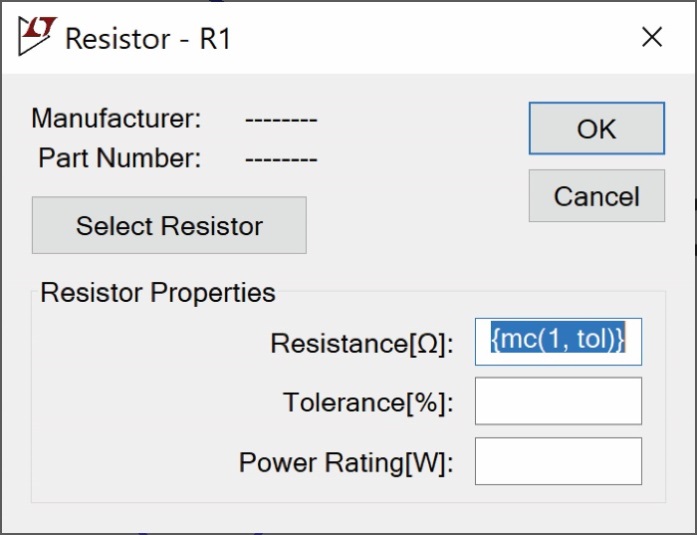
图23.在LTspice中编辑电阻值
输入{mc(1, tol)},将电阻标称值定义为1,蒙特卡罗分布由参数tol定义。参数tol被定义为SPICE指令。
可以使用控制栏中的SPICE Directive图标来输入图22所示的SPICE指令。如图24所示。


图24.在LTspice中输入SPICE指令
.meas命令可提供一个非常有用GUI,方便您输入相关参数。如图25所示。要访问此GUI,请输入SPICE指令作为.meas命令。右键单击.meas命令,将会弹出GUI。
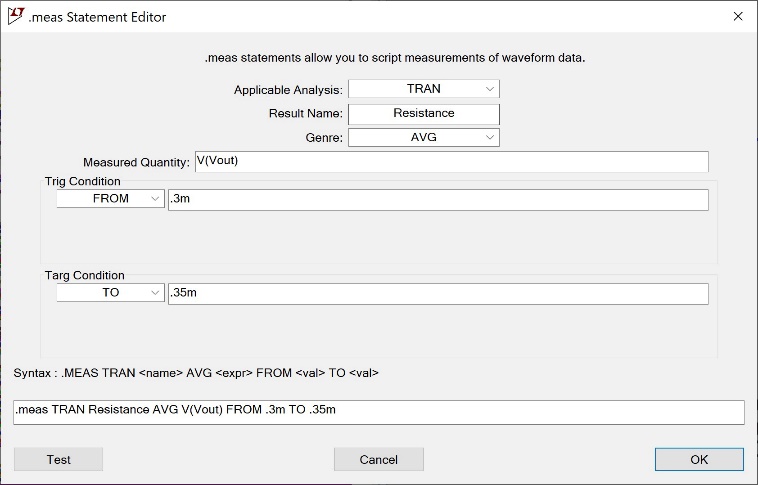
图25.输入相关参数的GUI
测量数据记录在SPICE错误日志中。图26和图27显示如何访问SPICE错误日志。
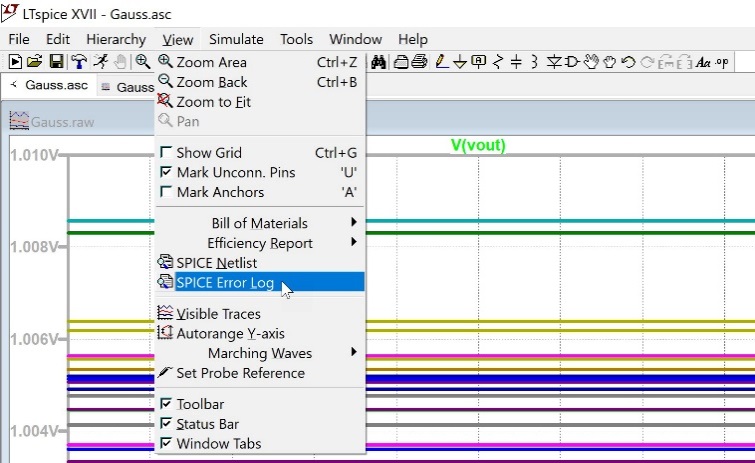
图26.访问LTspice错误日志
也可以右键单击原理图,直接从原理图访问该错误日志,如图27所示。
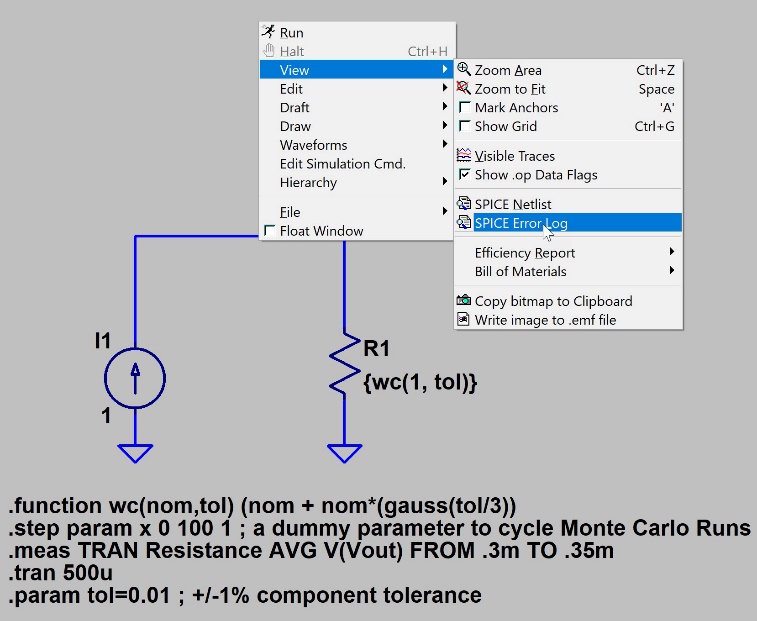
图27.访问LTspice错误日志
打开SPICE错误日志会显示测量值,如图28所示。可以将这些测量值复制粘贴到Excel中进行数值和图表分析。
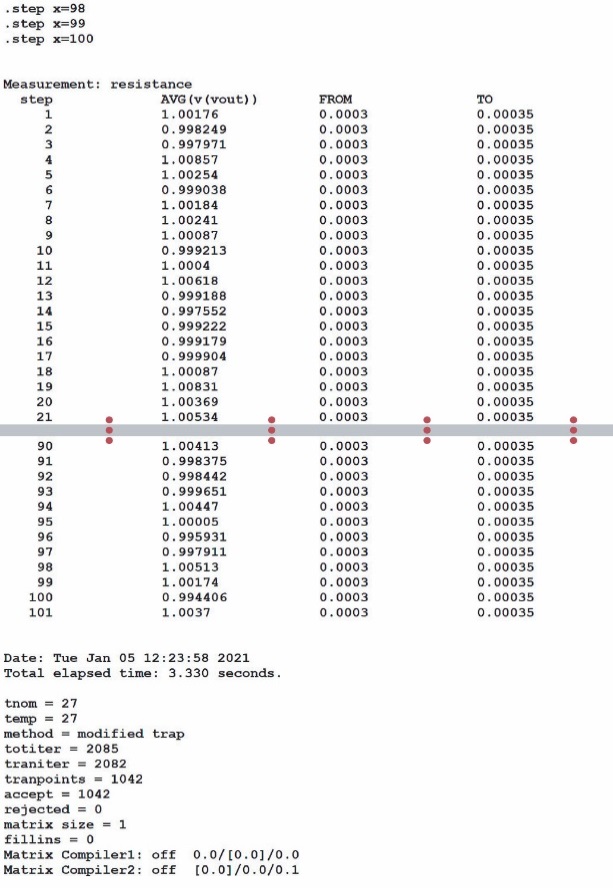
图28.SPICE错误日志图示,包含来自.meas命令的数据
Steve Knudtsen是ADI公司的一名高级现场应用工程师,工作地点在美国科罗拉多。他毕业于科罗拉多州立大学,拥有电子工程学士学位,自2000年开始,一直在凌力尔特和ADI公司工作。联系方式:steve.knudtsen@analog.com。
(原文标题:How to Model Statistical Tolerance Analysis for Complex Circuits Using LTspice)
 最前沿的电子设计资讯
最前沿的电子设计资讯