图1提供了滤波器部分的原理图,这是本文要讨论的主题。
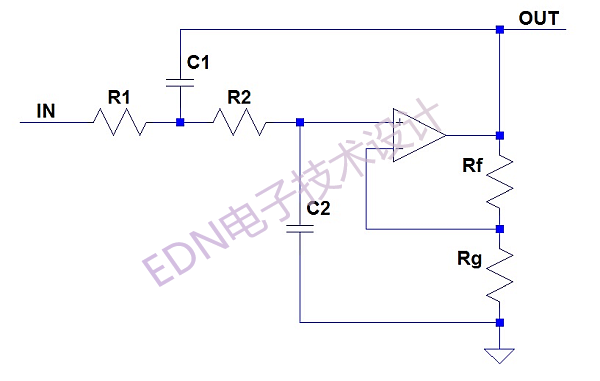
图1:SallenKey二阶低通滤波器原理图。
网上有许多不同的滤波器设计包。有些要求用户指定滤波器阶数和响应类型,例如Butterworth或Bessel。其它则要求通带纹波和宽度,以及阻带衰减,然后自动选择响应类型。这些可能会针对噪声、电压范围、低功耗或其它参数来优化。
其它设计包提供了更多的灵活性,而不只是处理响应类型,它们可让用户指定每个二阶滤波器的品质因数Q和谐振频率ω0(弧度/秒)。它们要求用户指定额外的参数组合来限定问题。这些参数可能包括DC增益和/或某些元件值。有了这些信息,就可以通过计算确定剩余的值。有时会提到Q和ω0对元件容差的敏感性问题。众所周知,滤波器在ω0时的幅度响应表现出最大的变化,即使对于合适的Q值也是如此,但是在单位DC增益(Rf/Rg = 0)的情况下,这种变化最小。这就要求C1 = 4·Q2·C2,这对于Q值较大时可能是有问题的。本文介绍的方法是当C1小于4·Q2·C2时,如何让滤波器响应灵敏度在频率ω0时达到最小。
滤波器配置的响应由下式给出:
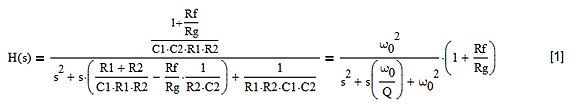
图2:以Q和ω0值表示的滤波器响应。
为了方便,我们在求解元件值之前先定义一些术语。适用于设计的电容值范围受到尺寸、价格和容差的限制。因此,我们要控制电容比,也希望控制DC增益,它等于1+Rf/Rg。所以我们定义:
![]()
图3:定义本文公式中将使用的一些术语。
从公式(1)可以看出,真正起作用的是电阻Rf和Rg之比Rr,而不是它们的绝对值。因此,一旦我们指定Rr,就可以选择数值大的Rf和Rg,以便使功耗最小,或者选择数值小的Rf和Rg,以便使噪声最小。如果我们还指定了C1和C2,则Cr也确定了。从这些值可以得出R1和R2:
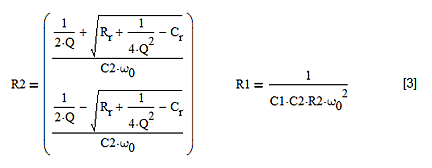
图4:用C2、Rr、Cr、Q和ω0计算R1和R2的值。有两组电阻值。
可实现性对Rr和Cr有一些约束要求。为确保平方根项及电阻R1和R2是实数,需要:
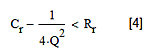
图5:所有滤波器的实现约束条件。
此外,从1/(2·Q)中减去平方根项的R2的表达式必须是正数,我们将其称为减法根。另一个称为加法根。所以,对于减法根,总约束是:
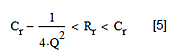
图6:R2的减法根构成的滤波器的实现约束条件。
公式(5)将R1和R2限制到减法根的一个小范围的值。稍后我们会看到,我们希望避免使用减法根实现滤波器,因为对于给定的Q、ω0、Cr和Rr,我们总是可以用加法根构建不太敏感的滤波器。
过去的设计中都是计算Q相对于电阻和电容每个值变化的灵敏度。但这里采用的方法是计算在频率ω0处滤波器响应幅度的灵敏度,ω0是变化最大的频率。这六个元件中每一个的灵敏度表达如下,其中Rr12=R2/R1:
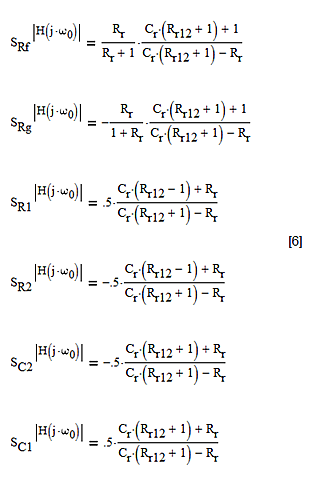
图7:谐振时滤波器响应幅度对每个元件值的灵敏度。
下一步是找出这些灵敏度的平方和,这样就可以得到尽可能小的值。结果(除以2)是:
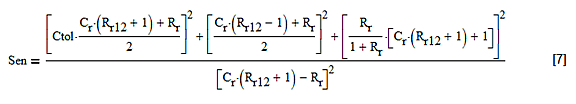
图8:谐振时滤波器对每个元件灵敏度的总和(除以2)。Ctol项是电容与电阻容差的比值。
请注意术语Ctol,这是电容容差与电阻容差的比值。例如,2.5%的电容容差和1%的电阻容差会得到2.5的Ctol值。在这种情况下,Ctol解释了电容值的更大变化。
我们希望确定公式的参数并消除Rr12,它可以用Cr和Rr表示。此外,由公式(3)给出的R1和R2电阻对的两个根的单独表达式是很有用的。我们也借此机会切换到平方和的平方根,因为这与所有元件的总灵敏度成正比。最后,我们希望仅绘制元件值的可实现范围。由于正在使用的图形包不会在图中画出虚数值,因此我们将√(-1)分配给不可实现的滤波器:

图9:谐振时滤波器响应幅值的每个元件灵敏度的平方和(除以2)的根。它包括R2的加法和减法根表达式。R1和R2用Cr和Rr表示。如前所述,术语Ctol也被采用。
图10显示随Rr变化的各种Cr值的滤波器的灵敏度。所示曲线的Q = 10和Ctol = 2.5,无论C2和ω0的绝对值如何,这些值都是有效的。实线是加法根灵敏度,虚线是减法根灵敏度。对于给定的Cr值,这两个根的曲线颜色相同。
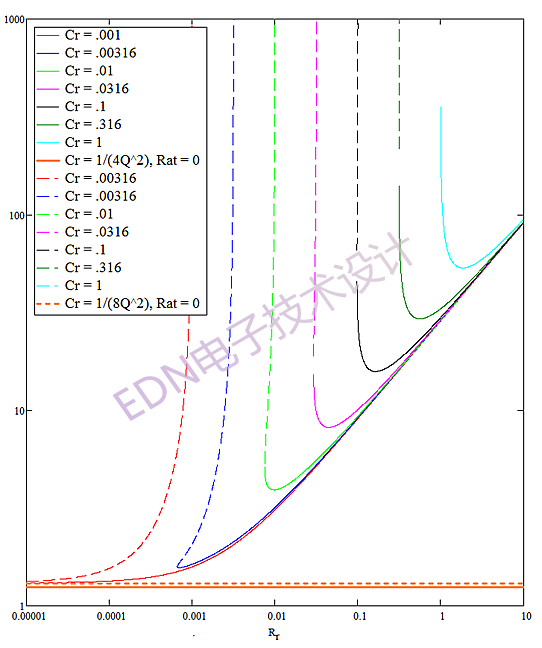
图10:被两部分滤波器分开的总灵敏度曲线,其中Q = 10和Ctol = 2.5,随着Rr变化,各种Cr值变化导致灵敏度变化。实曲线是加法根灵敏度,虚线是减法根灵敏度。对于给定的Cr值,这两个根的曲线颜色相同。
从图中可以清楚看出几点。首先是给定Cr的加法根的最小灵敏度总是小于相应的减法根的最小灵敏度。因此,我们不应该使用减法根的元件值构建滤波器。第二个观察结果是,一般来说,Cr = C2/C1的值越小,可以实现的灵敏度就越低(更好)。第三,直觉可能会告诉我们,最好的解决方案是使用最小的Rr值产生可实现的滤波器,但曲线显示并非这样。第四,底部的橙色水平实线是我们能达到的最好结果。它对应于单位DC增益,Rf短路和/或Rg开路,并对应于Cr = .25·Q-2,即C1 = 4·Q2·C2。如果我们认为使Cr值更小会进一步降低灵敏度的话,那么直觉再一次失败。当我们将Cr设为.125·Q-2时,橙色水平实线之上的橙色水平虚线会告诉真相。
我一直无法找到Rr最佳值的闭合解——曲线的鞍点,即对给定的Q、ω0、Cr和Ctol,滤波器的总灵敏度最小的位置。不过我提供了一个Excel表,它可以精确地将这个值限定在0.1%以内。
如果不对图11和图12中的各种滤波器设计进行蒙特卡洛分析,本文就不算完整。响应曲线以20dB的增量隔开,以便看得更清楚,而不会相互混淆。表1给出了图11曲线的元件值。这再次证明,对于元件灵敏度低的滤波器,减法根不是一个好的选择,同样电容也不是。我们还看到使用Rr = Rf/Rg的最优值与较低和较高值进行比较的可取性。利用Rf相对于Rg的最优值,可以计算Rr。
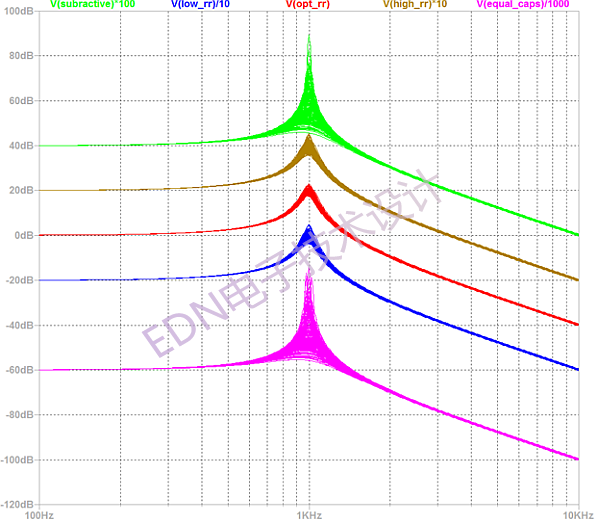
图11:各种滤波器设计的蒙特卡罗分析。
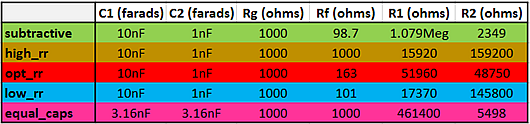
表1:图11中曲线的元件值。
图12:各种滤波器设计的蒙特卡洛分析,不同参数情况下的滤波器灵敏度存在差异,其中Q = 10,Ctol = 2.5,Cr = C2/C1比值分别为0.316、0.0316和0.00316。
图12显示了Q = 10,Ctol = 2.5,而Cr = C2/C1值分别为0.316、0.0316和0.00316时滤波器灵敏度的差异。这些已经用Rr的最优值计算出来了。表2列出了所有的滤波器元件值。

表2:所有的滤波器元件值。
我们只探讨了Q = 10和Ctol = 2.5时的滤波器设计。这似乎是说,设计中R1和R2的值相当接近最佳Rr值。这个推论对于Q和Ctol的所有值都正确吗?如果是这样,即便我们使R1和R2相等并计算出结果Rr,灵敏度增加的可能也微乎其微。当然,闭合公式适用于所有元件。不过,有了Excel表,目前的方法会得到最佳的灵敏度,而且很容易使用。
设计Sallen Key低通滤波器从指定Q和ω0开始。Sallen Key滤波器谐振时使响应灵敏度最小化至元件值的黄金标准是选择单位DC增益,其中Rf是短路和/或Rg是开路。这要求C1 = 4·Q2·C2。可以选择C2的值并计算C1。然后,R1和R2可以由公式(2)和(3)确定,其中R2应该选择加上而不是减去平方根。但对于高Q的情况,这可能并不总是一个理想的方法。在这些情况下,应在C1/C2具有可接受的最大比值时才选择C2。设计中我们还需要知道电容容差与电阻容差的比值Ctol。应该为这些值找到最佳比Rr = Rf/Rg,使用前面提到的Excel表也许能找到。Excel表可以计算R1和R2,还可以选择任意Rr值,为Rg和Rf,以及C1、C2、Q和ω0指定自己期望的值。然后,Excel表计算出R1和R2。
其它性能参数也可得到改善。使Rf||Rg = R1+R2,放大器偏置电流造成的失调将会最小。使C1||C2最大、Rf||Rg最小,元件阻抗和滤波噪声将会降至最低。使C最小、Rf||Rg最大,功耗会降至最低。
(原文刊登于ASPENCORE旗下EDN美国网站,参考链接:Designing second order Sallen-Key low pass filters with minimal sensitivity to component tolerances。)
《电子技术设计》2018年9月刊版权所有,禁止转载。
 最前沿的电子设计资讯
最前沿的电子设计资讯