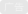
在这篇关于传输线理论的文章中，我们假设一根RG-58型同轴电缆，其特性阻抗为50Ω。其中，C代表单位长度的电容，本例中为每英尺30pF，特性阻抗Zo=sqrt(L/C)，其中L代表单位长度的电感。由此得出L=Zo²×C=每英尺75nH。
我们制作了一个非常简单的MultiSim SPICE模型，该传输线由图1左侧的50Ω源阻抗驱动，负载电阻我们将设置为几个不同的值，分别为10000Ω、50Ω，然后是5Ω，同时我们将在研究时域反射(TDR)时检查每个值的影响。
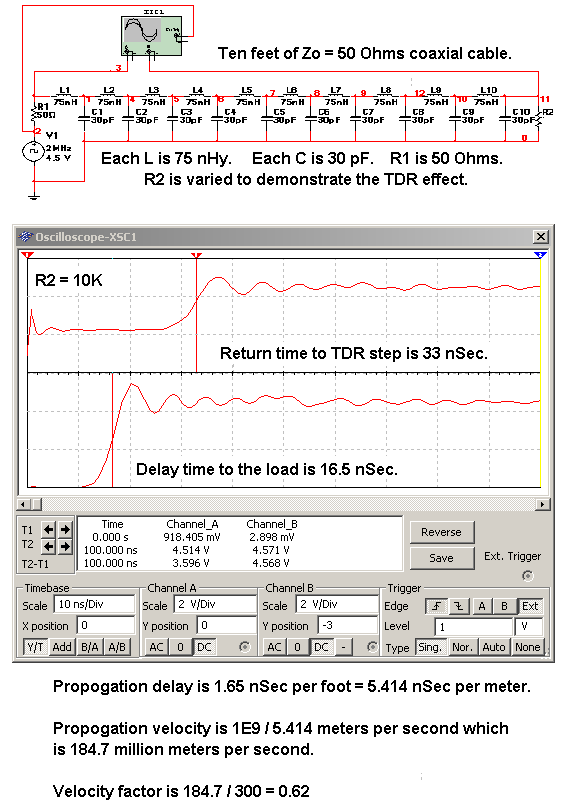图1：TDR结果来自MultiSim SPICE模型，该模型中的传输线由50Ω源阻抗(R1)驱动，其中负载电阻R2设置为10000Ω。
在图1中，使用方波信号源，我们看到信号沿传输线到达R2需要16.5ns。在此期间，V1和R1处的信号输入端呈现50Ω的输入阻抗，即电缆的特性阻抗Zo。
由于R2值与Zo不匹配，进入R2的能量传输不完整，部分到达的能量再次向左反射。当该反射再经过16.5纳秒到达R1(总传输时间为33纳秒)时，V1和R1对的阻抗会急剧上升，我们会看到传输线左端的输入电压也急剧上升。
根据传输时间可以计算出传输线的传播速度和速度因子，其速度几乎是自由空间中光速的三分之二，这与该电缆的公开数据相同。
在图2中，当R2为50Ω时，Zo与阻抗匹配，没有能量再次反射回来。当R2仅为5Ω时，Zo再次失配，能量向左反射回来，但左端的阻抗不升反降。
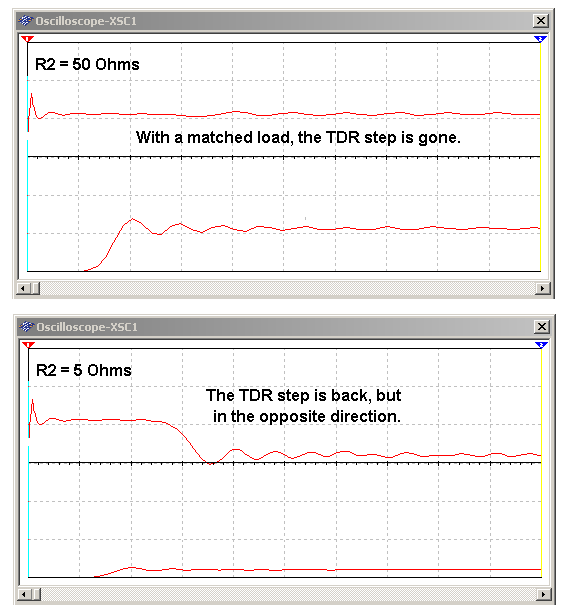
图2：负载R2=50Ω的TDR结果，显示匹配且没有能量反射回来，而R2=5Ω的TDR结果，显示不匹配且能量反射回来。
当然，这个SPICE模型非常粗糙，因为每个LC对代表一英尺长的电缆。如果采用一个更精细的模型，在每单位长度上加有更多的LC对，就能产生比我们这里展示的更好的波形结果。
不过这里只是为了说明清楚原理，还请大家多多见谅。
(原文刊登于EDN美国版，参考链接：Time domain reflectometry，由Ricardo Xie编译)
最前沿的电子设计资讯
