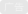
在本文中，我们将研究二极管在狄拉克脉冲反向偏压下的行为，然后再研究齐纳二极管的特殊情况。
图1所示电路中的二极管为反向偏置。施加的电压如下：
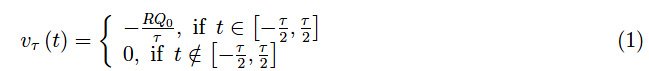
这里Q0>0是一个电荷的常量，而τ>0是信号的持续时间，其趋势如图2所示。
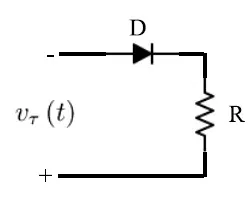
图1：二极管与电阻串联
我们打算研究当τ→0+时电路的行为，即当二极管受到狄拉克脉冲反向偏置时时的行为，更准确地说，这是一个确定电阻两端输出信号的问题。那么如果器件是齐纳二极管，又会发生什么情况呢？
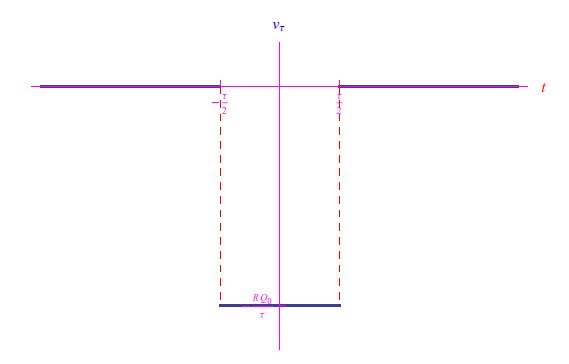图2：输入信号趋势
一种简单的解决方案是：由于狄拉克脉冲的持续时间无穷小，并且反向偏置二极管，因此电路中也会有同样无穷小的反向饱和电流通过。为了证明这个结论是错误的，让我们回顾一下关于结二极管的一些概念，众所周知，这种器件的电压-电流特性为：
其中，vD是二极管两端的电压，i0是反向饱和电流的绝对值，η是无量纲参数，在理想条件下等于1，VT是温度的等效伏特值，在室温下约为0.026V。根据公式(2)：
公式(2)准确描述了当vB<vD<+∞时二极管的行为，其中vB<0：
方程的垂直线(在直角坐标平面电压-电流中) i=vB是函数i(vD)图像的垂直渐近线，而vB就是所谓的击穿电压。
两个不同的过程导致了方程(4)所描述的强非线性行为：
齐纳效应是一种典型的类似于隧道效应的量子效应，过渡区较窄有利于从n区到p区以及从p区到n区的转变。
相反，当过渡区较宽并且载流子浓度的突然增加是由于破坏共价键的碰撞时，就会发生雪崩倍增。
这两种机制在技术上被用于实现能够稳定电压的器件，这种器件被称为齐纳二极管，因为人们认为击穿机制重点要归因于齐纳效应。
无论决定式(4)的机制是什么，都需要找到一个vD函数的解析表达式，使得当vD<0时，vB存在奇点(公式(4))；而在vD>0的范围内(直接极化)，奇点由公式(2)给出。让我们试试下面的方法：
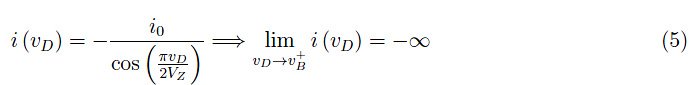
定义齐纳电压VZ=−vB。图3中显示了该函数的趋势，但当vD=0时，该函数不会抵消，图形就不能与vD>0范围内的部分连接起来了。不过问题不大，因为我们研究的是二极管在反向偏置下的行为。图4显示了固态二极管电压-电流特性的完整趋势，其中考虑到了不可避免的击穿。
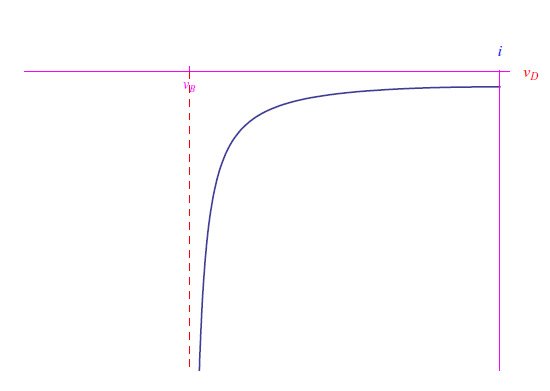图3：函数(5)的图像
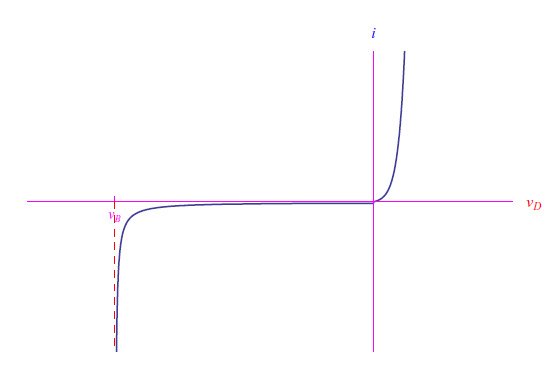图4：结二极管的典型电压-电流特性
在所绘制的图形中，|vB|相当高：这可以用于仿真基于SiC/GaN的器件。
我们成功重构了反向偏置电压-电流特性。为了从电压(1)过渡到狄拉克脉冲，必须对τ→0+进行操作，但对于τ=τmin>0的情况，有：
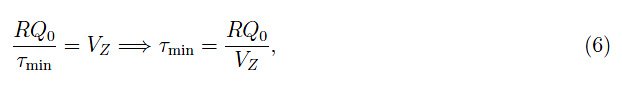
二极管击穿，如果没有电阻R，则i→−∞。电流值受电阻限制，但仍然很高，会损坏器件。
让我们继续讨论第二个问题。对于齐纳二极管，电压vτ(t)在vτmin(t)=−VZ时保持截止状态，因此它不会表现出狄拉克脉冲类型的行为。换句话说，对于齐纳二极管，不可能通过前面提到的临界操作(τ→0)来仿真狄拉克脉冲。
所有这些都可以通过将基尔霍夫第二定律应用于电路(1)进行分析研究，其中的器件为齐纳二极管。此过程会返回一个关于未知数i(t)的超越函数方程。通过适当地将未知函数无量纲化，可以轻松地以图形方式求解该方程。对于数值的细节，最好使用Mathematica等计算环境来获取输出信号的趋势，如图5所示。输出信号与输入信号具有相同的趋势，但有所衰减。
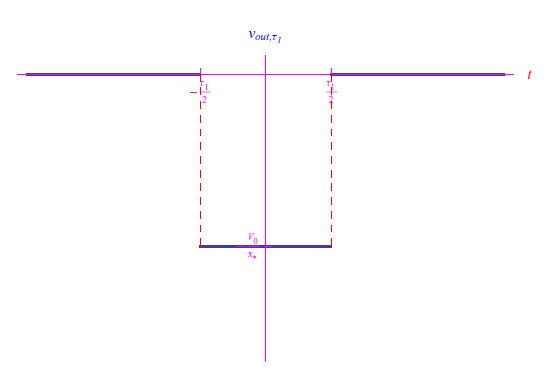图5：τ1=1.1s时的输出信号趋势
只有当特征量之间的不等式得到验证时，我们的结果才是有效的。不过很明显，只要二极管的典型参数符合这个条件，它就一定能得到验证，否则，齐纳二极管就会失效。
(原文刊登于EDN姊妹网站Power Electronics News，参考链接：Scientific Notes on Power Electronics: Zener Diode and Dirac Pulse，由Ricardo Xie编译。)
最前沿的电子设计资讯
