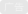
简单的RC电路无法用作逆变器。然而，之前文章中的一个练习提出了一些关于串联RC电路输出信号的有趣思考，该电路接受给定时间常数的指数阻尼RLC电路的输出信号作为输入。
我们之所以如此关注逆变器，是因为目前这些设备在光伏系统中至关重要。遗憾的是，要再现一个完美的正弦波形(频率f0=50/60Hz)非常困难，甚至是不可能的。这意味着不可避免地存在频率为f0倍数的谐波，如果系统没有得到恰当的屏蔽，这些频率的谐波会产生电磁辐射，从而干扰其他发射/接收设备。
练习1：考虑将以下输入应用于时间常数τ=RC的积分电路：
其中：A=10V，τ0=1s为特征时间，T=8s为周期。信号行为如图1所示，该输入是时间常数为τ0的阻尼RLC电路的输出，该电路每8秒恢复到初始状态，因此，输入信号的频率为f0=1/8Hz。
编写一个Wolfram机程序，使其能够重构输出信号，区分τ/=τ0和τ=τ0的情况。有可能用这样的装置制造出逆变器吗？
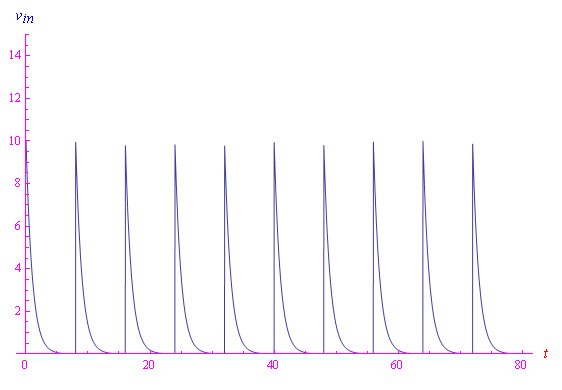图1：信号趋势(公式(1))
本练习的(表面上)难点在于R和C的值未知，但它们的乘积RC=τ(自由参数)。在之前的文章中，我们看到，基于基尔霍夫第二定律的微分方程包含时间常数τ和电阻值R，我们必须在此基础上添加电荷的初始条件，该初始条件可以不为零(在本例中，电容器最初带电，因为它之前经历了一次瞬态)。
通过解析求解该问题，在最后一步，即计算输出信号时，变量R就会消失，从而解决掉该问题。然而，更简单的方法是直接写出一个微分方程，其中未知函数不是电容器极板上的电荷q(t)，而是电容器极板上的电位差，即输出vout。
这得益于电荷与电容器电容之间的线性关系：q=Cvout。用一些简单的步骤即可得出上述微分方程，该方程必须用明显的初始条件vout(0)=Cq(0)≡v(0)求解，该初始条件可任意赋值。
然而，有趣的情况是电容器最初没有负载，此时vout(0)=0。这样，图2显示了该问题在初始值下的唯一解，“积分电路”一词的含义也由此而来，因为输入是由积分处理的。
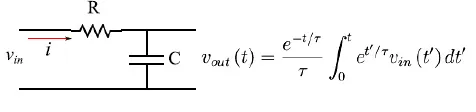
图2：输出电压(练习1)
这里出现了一个问题：当积分电路的时间常数与输入的时间常数一致时，函数vout(t)的解析表达式不能用于τ=τ0，因为该表达式返回的是不定式0/0，在这种情况下，需要将τ=τ0的微分方程改写，然后再进行积分。
在图3中，我们比较了输出趋势与输入趋势，τ的值取以下值(四舍五入到小数点后第三位)：τ=0.002,1.002,2.002,3.002s。请注意，第二个值非常接近τ0。因此，我们看到，当τ趋向于零时，输出趋向于输入。在相反的极限(τ→+∞)下，输出趋向于相同的零信号，正如预期的那样，因为在此极限下电阻或电容趋向于+∞。
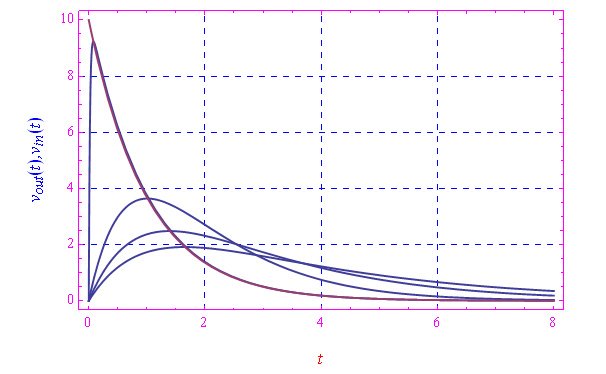图3：蓝色图是vout(t)随τ变化的曲线
关于能否实现逆变器，答案是否定的，因为这需要更复杂的设备。从数学上讲，我们从被积函数的符号(图2)可以看出，它显然为正。根据定积分的已知性质，我们可以得出，当积分符号为正时，积分在[0,t]区间内定义。
重置τ=τ0的微分方程并求解，我们得到图4和图5的图形，其中我们首先在周期间隔内比较vout(t)与vin(t)，然后在[0,80s]内比较。
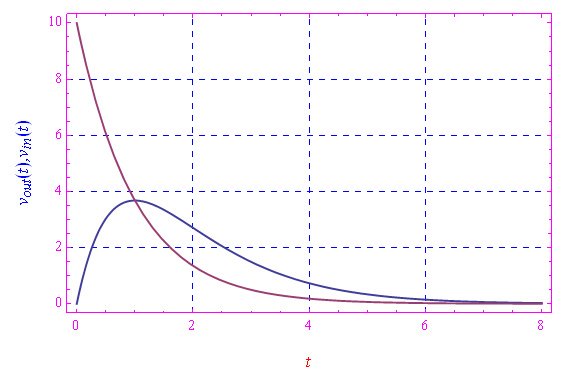图4：蓝色曲线表示τ=τ0时的vout(t)
图5：蓝色曲线表示τ=τ0时的vout(t)
一旦使用合适的Wolfram机建立微分方程，并将τ作为自由参数，当我们尝试绘制τ=τ0的解的图形，内核将尝试通过除以0来消除不定式0/0，进而报错。我们可以将WM(Wolfram机)拆分为两个不同的WM，一个用于τ/=τ0，另一个用于τ=τ0，但设置一个IF循环更好，正如我们从图6中看到的那样，其中我们突出显示了相应Mathematica代码的一些重要方面。
图6：基于IF循环的Wolfram机
首先，不能使用延迟赋值“:=”，它会指示内核仅在新输入调用时才确定相应的表达式(函数、指令或其他)，这种赋值类型常用于递归程序和缓存技术，但在存在导数等类似情况时会产生问题。
例如，如果我们使用延迟赋值来确定给定函数f(x)的导数，然后询问该导数在给定点x0的值，内核会首先替换f(x)解析表达式中的值x0，然后再计算导数，此时会报错(实际上应该为零，因为这是一个常数的导数)。您可以使用功能强大的Evaluate指令，或者更简单地使用立即赋值“=”。
对于微分方程来说，情况更为复杂，仅仅使用立即赋值是不够的，需要插入Evaluate函数，并且我们使用了后缀符号，以避免括号过多。代码解释正确，我们通过将其与解析结果进行比较进行了一些检查。
众所周知，IF循环是传统编程语言的典型语法，在Mathematica中，它具有以下语法(星号之间的字符串是内核会忽略掉的注释条目)：
If[ (*condition*) expr, (*then*),
t (*else*) p
]
That is, if expr is True, the kernel executes t, otherwise it executes p. For example:
In[1]=test[x_] := If[ x^3 > 14,
Print[“Correct answer. It turns out:” , x^3], Print[“Wrong answer”]
]
In[2]=test[2]
Wrong answer In[3]=test[3]
Wrong answer Correct answer. It turns out:216
尽管Mathematica/Maple、Maxima等“盒装”软件就像是黑匣子，不允许用户直接访问代码，但在许多应用中，它们非常灵活，只用几行代码就可以解决复杂的问题(这是Fortran或C等传统编程语言无法实现的)。
(原文刊登于EDN姊妹网站Power Electronics News，参考链接：Scientific Notes on Power Electronics: Is It Possible to Make an Inverter with an RC Circuit?，由Ricardo Xie编译。)
最前沿的电子设计资讯
